7.9, #21. If x ³ 3, then x² ³ 3x and e^-x2 £ e^-3x. Thus

7.9, #22. [(2x²+1)/( 4x⁴+4x²-2)] behaves like [(2x²)/( 4x⁴)] = [1/( 2x²)] for large x. By the p-test integral (a) should converge while integral (b) should diverge (since (1/2x²)^1/4 = 1/2^1/4x^1/2). Indeed, 4x²-2 ³ 0 for x ³ 1, so

7.9, #25. The tangent line approximation 1+t to e^t at t = 0 lies below the graph of e^t since the graph of e^t is concave-up. Thus 1+t £ e^t for all t. Substituting t = 1/x in this inequality gives 1+(1/x) £ e^1/x or e^1/x-1 ³ (1/x). Thus

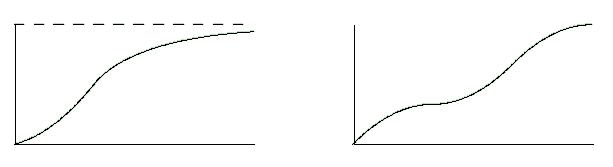
7.10, #2: F(x) starts at (0,0) and is increasing, concave-up on its initial segment, concave-down on its second segment, where it approaches a horizontal asymptote.

7.10, #3. F(x) starts at (0,0) is increasing, concave-down on its initial segment, concave-up on its middle segment, concave-down on its last segment.

7.10, #6. Note the following features of the six slope fields: (I) and (III) have horizontal slopes for large |x|. (II) and (IV) have steep slopes for large |x| with (IV) having almost vertical slopes. Lastly, (V) and (VI) are the only slope fields with negative slopes. It follows easily that (d) e^-0.5xcosx is matched with (V) and (f) -e^-x2 with (VI). The difference between (I) and (III) is that of scale with respect to the x-direction. So (b) e^-2x2 and (c) e^-x2/2 are matched respectively with (I) and (III). Finally, (a) e^x2 is matched with (IV) and (e) (1/(1+0.5cosx)² with (II). Indeed, since 1/2 £ 1+0.5cosx £ 3/2, it follows that 4/9 £ 1/(1+0.5cosx)² £ 4. Thus the steepness of the slope field of (e) is bounded, and the match must be (e) with (II) and (a) with (IV).

7.10, #8. [d/ dx]ò₀^xÖ{3+cos(t²)} dt = Ö{3+cos(x²)}.

7.10, #10. [d/ dx]ò_0.5^xarctan(t²) dt = arctan(x²).