6.4, #22. Noting that the derivative of sin(t²) is 2tcos(t²) we have that sin(t²) is an antiderivative of 2tcos(t²). Thus ò2tcos(t²) dx = sin(t²) + C.

6.4, #23. See the previous problem. From it we see that the derivative of ¹/₂sin(t²) is tcos(t²). Thus ¹/₂sin(t²) is an antiderivative of tcos(t²). Observe that òtcos(t²) dx = ¹/₂sin(t²) + C.

6.4, #30. An antiderivative of F¢(x) = e^x has the form F(x) = e^x+C. The condition F(0) = 2 translates to 1+C = 2. Thus C = 1 and F(x) = e^x+1.

6.4, #31. An antiderivative of x² has the form F(x) = ¹/₃x³+C. The condition F(0) = 2 translates to 0+C = 2. Thus C = 2 and F(x) = ¹/₃x³+2.

6.4, #32. An antiderivative of F¢(x) = cosx has the form F(x) = sinx+C. The condition F(0) = 2 translates to sin0+C = 2. Thus C = 2 and F(x) = sinx +2.

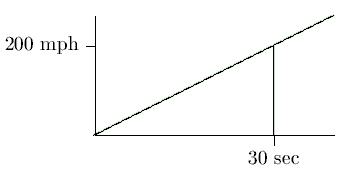
6.4, #50. Acceleration is constant, say a miles/hr². The plane has initial velocity v₀ = 0 mph and initial position s₀ = 0. So the velocity and position functions of the plane on the runway are v(t) = at and s(t) = (1/2)at². The plane reaches velocity 200 mi/hr in 30 seconds, that is, 200 = v(30/3600) = a×(30/3600). Thus a = 24000 mi/hr². Since s(30/3600) = (1/2)×24000×(30/3600)² = 5/6 miles, the length of the runway is at least 5/6 miles.

A shorter proof: The problem is to compute the distance the plane has traveled when its velocity is 200 mi/hr. The graph of velocity as a function of time is

6.4, #54. The height of the rock t seconds after being thrown is s(t) = v₀t-(1/2)gt² feet, where s(t) is measured from the initial position of the rock, v₀ is the initial velocity of the rock, and g = 32 ft/sec². The rock reaches its highest height h when s¢(t) = 0, that is, when t = v₀/g. Thus h = s(v₀/g) = v₀(v₀/g)-(1/2)g(v₀/g)² and v₀² = 2hg. In part (a) h = 100, so v₀ = Ö{200×32} = 80 ft/sec. In part (b) g = 5 and v₀ = 80, so h = (80)²/(2×5) = 640 feet.

6.Rev, #36. v = -32t + v₀ = -32t + 160. We plot v (vertical axis) versus t (horizontal axis). The graph of v is a straight line with slope -32 and v-intercept 160.

a) The maximum height occurs when v = 0. Thus 32t = 160 which means that t = 5.

b) The object hits the ground when the area above the t-axis is equal to the area below the t-axis. This happens when t = 10.

c) The maximum height is the area bounded by the graph of v = -32t + 160, the t-axis and the vertical lines t = 0 and t = 5. This region is a triangle with base of length 5 and height 160. Thus the maximum height, or area, is [160 ×5/ 2] = 80 ×5 = 400 feet per second.

d) By antidifferentiation we compute the greatest height by

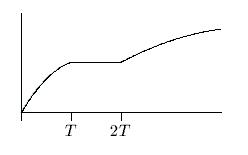
6.Rev, #42. The height H increases until it reaches the top of the inverted ``vee''. Say this happens for time 0 £ t £ T. Then H is constant for time T £ t £ 2T as water fills the corresponding space on the right. H increases again for t ³ 2T, but at a slower rate than before since the space being filled corresponds to the entire width of the container. Note too that the container widens from bottom to top, so the increasing portions of the graph are concave-down.