6.2, #4. |x| is non-negative, so ò_-1¹ |x| dx is the area of two triangles: the first has sides on the lines y = -x, x = -1, y = 0; the second has sides on the lines y = x, x = 1, y = 0. Clearly ò_-1¹ |x| dx = 1

6.2, #5. a) [1/( Ö{2p})]ò³₁ e^{-[(x2)/ 2]}dx = [1/( Ö{2p})]ò³₀ e^{-[(x2)/ 2]}dx -

[1/( Ö{2p})]ò¹₀ e^{-[(x2)/ 2]}dx = 0.4987 - 0.3413 = 0.1574.

b) [1/( Ö{2p})]ò³_-2 e^{-[(x2)/ 2]}dx = [1/( Ö{2p})]ò⁰_-2 e^{-[(x2)/ 2]}dx + [1/( Ö{2p})]ò³₀ e^{-[(x2)/ 2]}dx

= [1/( Ö{2p})]ò²₀ e^{-[(x2)/ 2]}dx + [1/( Ö{2p})]ò³₀ e^{-[(x2)/ 2]}dx = 0.4772 + 0.4987 = 0.9759.

6.3, #2. F¢(x) = f(x) is negative on [0,1] and positive on

[1,¥),

so F(x) is decreasing on (0,1) and increasing on (1,¥).

F¢¢(x) = f¢(x) = 1 is always positive, F(x) is concave up on

[0,¥).

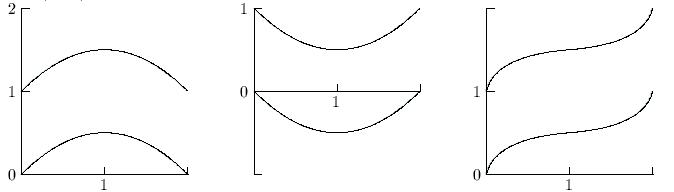
6.3, #3. F¢(x) = f(x) is positive on [0,¥),

so F(x) is increasing on [1,¥).

F¢¢(x) = f¢(x) is -1 on [0,1) and 1 on (1,¥). So F(x)

is concave-down on (0,1) and concave-up

(1,¥).

6.3, #6 F¢(x) = f(x) > 0 for x > 0 so F(x) is increasing. F¢(x) = f(x) is also increasing so the graph of y = F(x) is concave up.

6.3, #11. The cork is oscillating relative to the sea floor. Its position above the sea floor is the signed area bounded by the velocity graph. So at point B the cork is at its crest, at point D the cork is at its trough. At points A and C the cork is halfway between its crest and its trough. The acceleration is zero at points A and C, where the tangent line to the velocity graph is horizontal. The function giving the position of the cork above the sea floor has form -cost+C for some constant C.